Start
Research
Publications
Statistics playground
Teaching
CV
Contact
Stochastic processes
For an overview of my interests in stochastic processes see here.
Total regression
For an overview of fitting data when both axes x and y have measurement errors check my page on total regression here.
Stable least-squares fitting
For an overview of my interests in stable least-squares fitting see here.
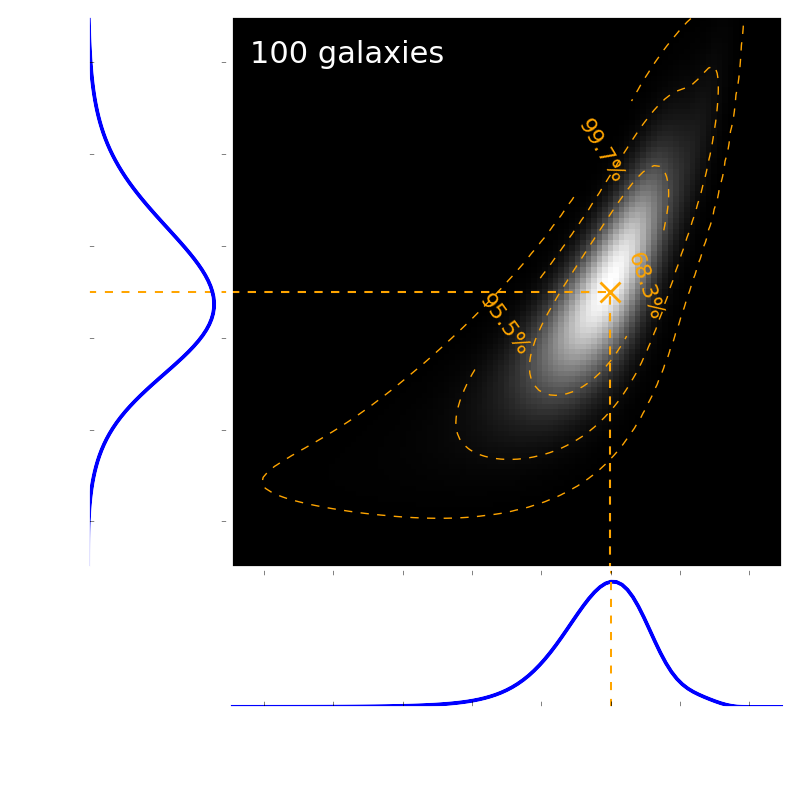 Figure 1. Estimating a Schechter luminosity function from just 100 galaxies! Shown is the likelihood manifold of the two model parameters of a Schechter function. The simulation used measurement errors of 0.3 magnitudes and is averaged over 100 noise realisations, i.e., error contours contain both estimation uncertainty and sampling/shot noise. The dashed orange lines indicate true values.
Figure 1. Estimating a Schechter luminosity function from just 100 galaxies! Shown is the likelihood manifold of the two model parameters of a Schechter function. The simulation used measurement errors of 0.3 magnitudes and is averaged over 100 noise realisations, i.e., error contours contain both estimation uncertainty and sampling/shot noise. The dashed orange lines indicate true values.
Galaxy luminosity functions without binningThat project is very similar to the IMF project. In fact, the methodological problem is virtually identical. Only the astrophysical background is different.
However, in this case, the method is already in application and will soon produce first astrophysical results.
Figure 1 shows an example of estimating the Schechter luminosity function of only 100 galaxies. With binning, this would be a hopeless enterprise. Without binning, we obtain an unbiased estimate.
Comparing population proportions, e.g., are galaxy mergers more frequent in active than in inactive galaxies?
That is actually a fairly simple methodological problem that can be solved accurately, i.e., without any approximations. The trick is to interpret the merger events in active and inactive galaxies as Bernoulli trials. The comparison then works by convolving the beta distributions of both samples with each other.
This simple methodological solution has already been applied in two publications and has spawned two further proposals for observation time.
Currently, I am writing up an arxiv manuscript explaining the foundations of the method. It will also contain a complete set of code - ready for use.
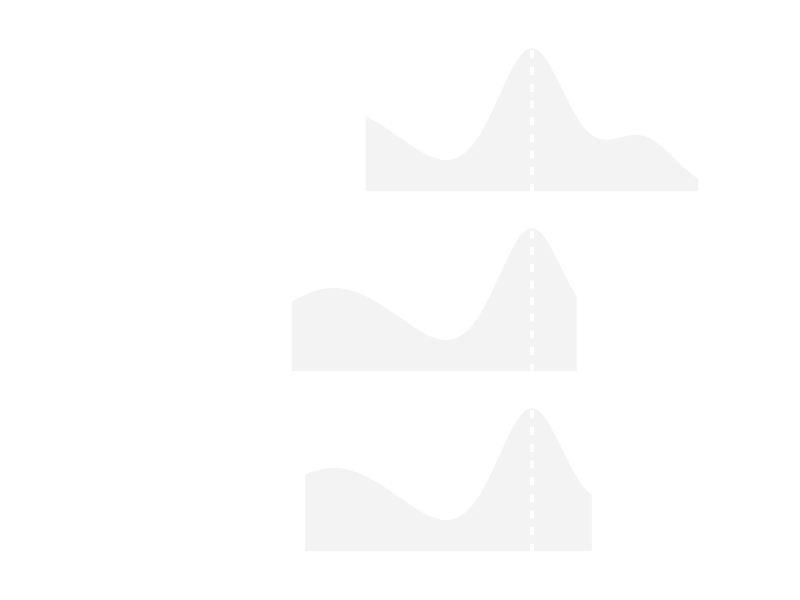 Figure 2. Three different types of one-dimensional 68% confidence intervals for an unfriendly likelihood function.
Figure 2. Three different types of one-dimensional 68% confidence intervals for an unfriendly likelihood function.
Error estimationWhile reading through the astronomical literature, I encountered lots of adventurous methods to estimate errors of fit parameters. Therefore, I wrote a short arxiv manuscript how to do it properly, which is meant to help PhD students and others interested in this subject. Figure 2 shows a simple example.
Monte-Carlo methods
After computers became sufficiently powerful in the 1990s, MC methods experienced a hype. However, there is lots of mythology associated with these methods, too. In the course of my research, I worked into this subject from the perspective of parameter/error estimation. Here are some of my conclusions:
- "MCMC can find the global optimum." You still find statements like that in the literature. In theory, this is correct, if you let the MCMC run for infinite time. In practice, you can only run it for a finite time - which is most often severely limited. Hence, this nice theoretical result is rather useless in practice. While MCMC may not run into the next best local optimum (like downhill gradients), it will probably run into the second- or third-best local optimum until you stop it.
- Convergence tests of MCMC are "black magic". Some diagnostic tools appear to work well, but one can always easily construct (realistic) situations where they fail miserably. If you really need convergence, you have to check it yourself very carefully. (The crux here is that MCMC actually is a tool for numerical integration, which is often "abused" for optimisation instead.)
- I also played with multi-state slice sampling MCMC algorithms, which are said to explore highly degenerate likelihood manifolds more efficiently than normal MCMC. While that is true, it remains unclear from what parent distribution multi-state algorithms are actually sampling. At least, it can be easily shown that they do not sample from the likelihood function of the data.
- The best MCMC algorithm in my opinion is the EMCEE, which is an ensemble MCMC that in my experience exhibits very efficient convergence. We employ EMCEE in our work for Gaia, where we fit the spectra of ~1 billion stars.
- Convergence tests of MCMC are "black magic". Some diagnostic tools appear to work well, but one can always easily construct (realistic) situations where they fail miserably. If you really need convergence, you have to check it yourself very carefully. (The crux here is that MCMC actually is a tool for numerical integration, which is often "abused" for optimisation instead.)
In the case of linear models and Gaussian data noise, the likelihood is a pure Gaussian with a single well-defined maximum. As soon as models become nonlinear or data noise non-Gaussian, that changes. Nevertheless, we would like to find the global optimum, instead of a local one.
MCMC methods cannot do the trick, since they are started at a single location and are usually not run long enough to completely explore the likelihood manifold.
I therefore worked a little bit with nested sampling algorithms. They have a better chance to identify the global optimum. However, their time complexity scales exponentially with number of model parameters - like a brute-force grid - because the number of required "livepoints" scales exponentially.
Another approach to identify global optima are genetic algorithms, which mimic biological evolution via processes equivalent to mutation, reproduction and selection according to fitness. However, so far I had no time to play around with these methods.