Stars that approach within one parsec of the Sun:
New and more accurate encounters identified in Gaia Data Release 3
C.A.L. Bailer-Jones
Close encounters of stars to the Sun could affect life on Earth through gravitational perturbations of comets in the Oort cloud or exposure to ionizing radiation. By integrating orbits through the Galactic potential, I identify which of 33 million stars in Gaia DR3 with complete phase space information come close to the Sun. 61 stars formally approach within 1 pc, although there is high confidence in only 42 (two thirds) of these, the rest being spurious measurements or (in) binary systems. Most of the stars will encounter within the past or future 6 Myr; earlier/later encounters are less common due to the magnitude limit of the Gaia radial velocities (RVs). Several close encountering stars are identified for the first time, and the encounter times, distances, and velocities of previously known close encounters are determined more precisely on account of the significantly improved precision of Gaia DR3 over earlier releases. The K7 dwarf Gl 710 remains the closest known encounter, with an estimated (median) encounter distance of 0.0636 pc (90% confidence interval 0.0595-0.0678 pc) to take place in 1.3 Myr. The new second closest encounter took place 2.8 Myr ago: this was the G3 dwarf HD 7977, now 76 pc away, which approached within less than 0.05 pc of the Sun with a probability of one third. The apparent close encounter of the white dwarf UPM J0812-352 is probably spurious due to an incorrect RV in Gaia DR3.
- Article: Astrophysical Journal Letters, 935, L9, (2022; submitted 18 June 2022)
[PDF] [ADS] [journal] [arXiv] [poster] - My warning in the paper not to trust the Gaia radial velocity - and therefore the close encounter - for the white dwarf UPM J0812-3529 has been vindicated by a new spectrum and analysis by Landstreet et al. (2023).
- Some extra tables and plots for all 61 apparent encounters. Note that
19 of these are probably not real encounters, as listed in the
paper.
- Tables 1 and 2
combined (CSV file) [new version on 2022-07-18]
- Table at CDS (Table name is J/ApJ/935/L9)
- As Figure 2 in the paper, but now labelling all encounters.
- 1D distributions of perihelion
time, distance, velocity for the surrogates for each star (ordered
as in tables)
Blue line = median; red line = from linear motion approximation using nominal data (sometimes outside the plotting range) - 2D plots of perihelion distance vs time for all surrogates for each encountering star (ordered as in tables)
- Tables 1 and 2
combined (CSV file) [new version on 2022-07-18]
The plots below shows the location of the star at perihelion (closest encounter) relative to the Sun in Galactic Cartesian coordinates. x points away from the Galaxy centre in the plane of the Galaxy in the phi=0 direction (the longitude of the Sun); z points perpendicularly out of the Galactic plane towards the north Galactic pole; y completes the right-handed coordinate system (so it points in the opposite direction of the rotation of the Galaxy). If the Sun was at the centre of the Galactic plane then the x axis would pass through the Sun, but in the model used in the paper the Sun is (at the present time) above the Galactic plane. Thus the xy-plane is the Galactic plane, and the xz- and yz-planes are the two "side" views.
Each point is one surrogate star, i.e. a random realization of the star's 6D coordinates (drawn from the uncertainties in position and proper motion) which has been integrated through the Galactic potential to perihelion. The actual position of the Sun relative to the Galactic centre is slightly different for each surrogate because the time of the encounter is different for each surrogate. So each encounter occurs in a frame which is slightly offset from the other, but all with the same orientation, which are then superimposed here.
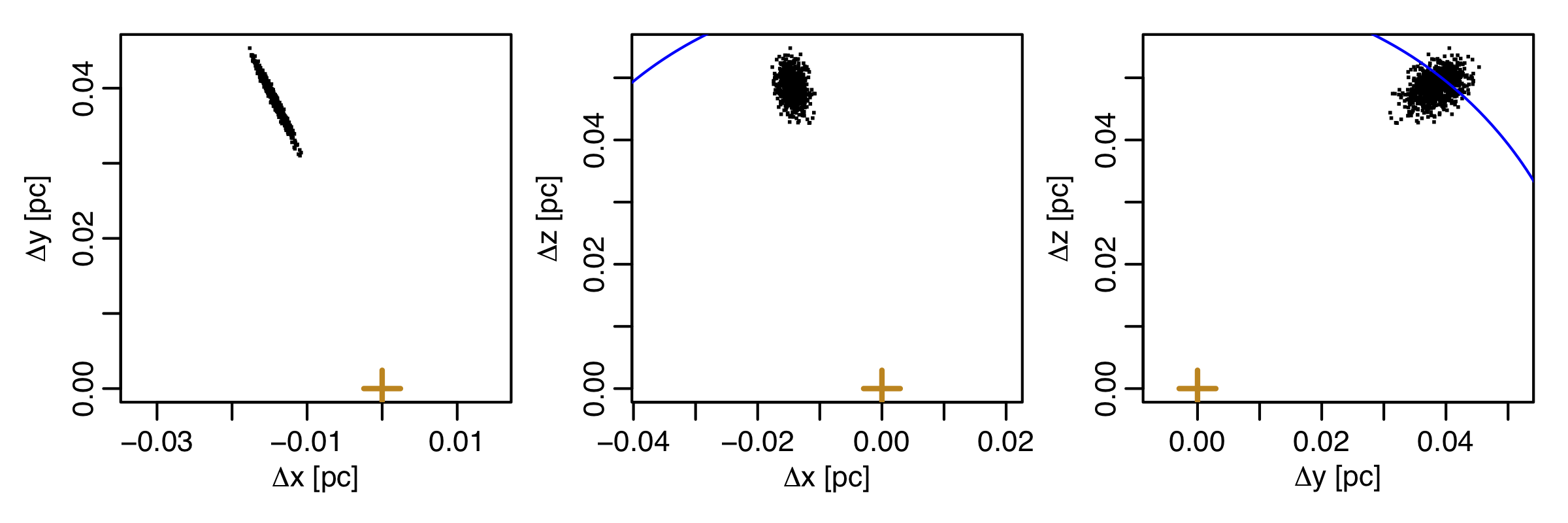 |
The plot above is for Gl 710 (Gaia DR3 4270814637616488064), the closest encountering star. The orange cross is the Sun (origin), each black point a surrogate. The blue arc is a cricle of radius equal to the median encounter distance, in this case 0.0636 pc. In the Galactic plane (left), we see that the surrogates form a long thin distribution poined at the Sun. In the other two projections the surrogates are more circular. Which projections are more elongated and which more circular depends on the fractional uncertainty of the velocity of the star in the x, y, z directions, which are not parallel to the proper motion and radial velocities (as those are defined in spherical polar coordinates relative to the Sun). The "side" projections show that the surrogates are all passing above the Sun.
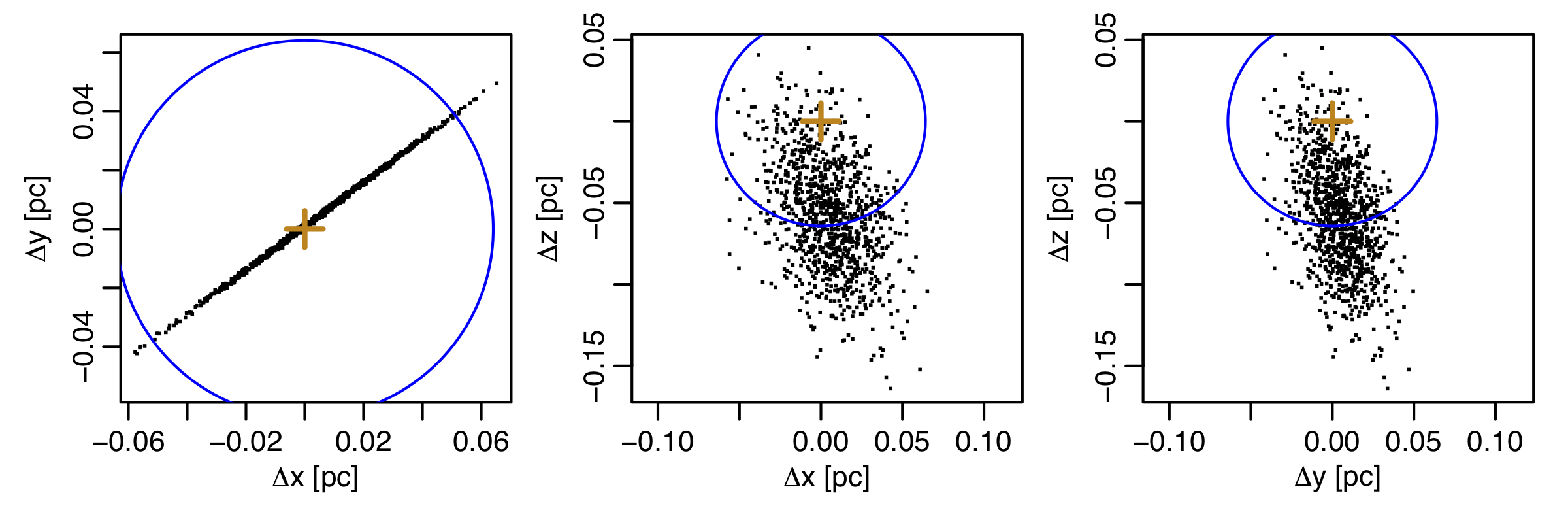 |
The plot above is for HD 7977 (Gaia DR3 510911618569239040), the
second closest encounter. The median encounter distance (radius of
blue circle) is 0.0641 pc. Here, the projected positions of the
surrogates in the Galactic plane (left) are on both sides of the
Sun. This plot illustrates the point discussed in the last paragraph
of section 3 of the paper: If we decided to average the 2D positions
in this plot, we would get an average position very close to zero,
because the surrogate pass on both sides of the Sun, and so many
positive and negative quantities average out: we get