Gaia is performing the most detailed and accurate astrometric survey ever attempted. It will measure distances to stars using the parallactic effect: the apparent motion of stars due to the orbit of the observing platform about the Sun. Gaia achieves this this by measuring angles to very high accuracy, some ten microacrseconds; the angular size of a 1 Euro coin on the moon seen from the Earth. By measuring the positions over a period of five years, Gaia will also measure their proper motions (space velocities). This will produce a three dimensional map of 1 billion stars in the Galaxy, complete with kinematics accurate to a few km/s. Armed with this, astronomers will study the structure, origin and evolution of our Galaxy, including the quantity and distribution of elusive dark matter. By detecting and mapping the streams of stars (believed to be remnants of galaxies which merged with ours) in the Galactic disk and halo, we can reconstruct the history of how our galaxy was built up. Gaia will also be able to detected the tiny wobble of stars due to unseen orbiting planets, and is expected to detect over one thousand exoplanets in this way. This method has the advantage over the radial velocity method of being useful for stars over the whole HR diagram, and gives actual mass estimates rather than lower limits. Gaia will also measure the General Relativistic bending of light on solar system size scales with an accuracy not yet achieved, providing new tests of this theory, as well as detect large numbers of potentially impacting Near-Earth Asteroids.
Distance estimates are vital to almost every aspect of astrophysics, converting angular scales to physical ones and yielding intrinsic (rather than apparent) luminosities of objects. Astrometry is the only way of obtaining distances without making assumptions about the source. The high distance accuracy on large number of objects promises to revolutionize many branches of astrophysics. As an example, an accuracy of 1% or better will be achieved on some 11 million stars as far away as 1kpc. This compares to fewer than 200 stars with a parallax of this accuracy obtained from Hipparcos, all of which lie within 10pc.
Gaia is a mission of the European Space Agency. The data processing will be undertaken by a pan-European consortium, the Gaia Data Processing and Analysis Consortium (DPAC). On account of the complexity and volume of data, this is an enormous task, and the consortium comprises over 400 people in over 20 countries.
The Gaia astrometric data can only be properly exploited once we know the
physical properties of the stars observed. For this reason Gaia will measure
low resolution optical spectrophotometry of every source it observes (Figure
1), plus high resolution radial velocity spectra. One of the eight
coordination units of the DPAC, lead by Coryn Bailer-Jones at MPIA, is
dedicated to extracting astrophysical information from these (other
coordination units work on the extraction, processing and calibration of these
spectra). A group of five scientist at MPIA, funded by the DLR and MPIA,
focuses on two particular aspects of this work. The first is the discrete
classification of objects into star, galaxy, quasar etc. Due to the nature of
Gaia observations, there will be limited or no spatial shape on the sources,
so classification can only be done via the spectrum. The second task is the
estimation of stellar astrophysical parameters, in particular the effective
temperature, surface gravity, composition and line-of-sight interstellar
extinction. These are the fundamental parameters which we need to derive
masses and ages and thus convert the Gaia spatial/kinematic map into a
mass/age/composition one. With this we will learn about the chemical evolution
of the Galaxy, changes in the star formation rate etc.

|
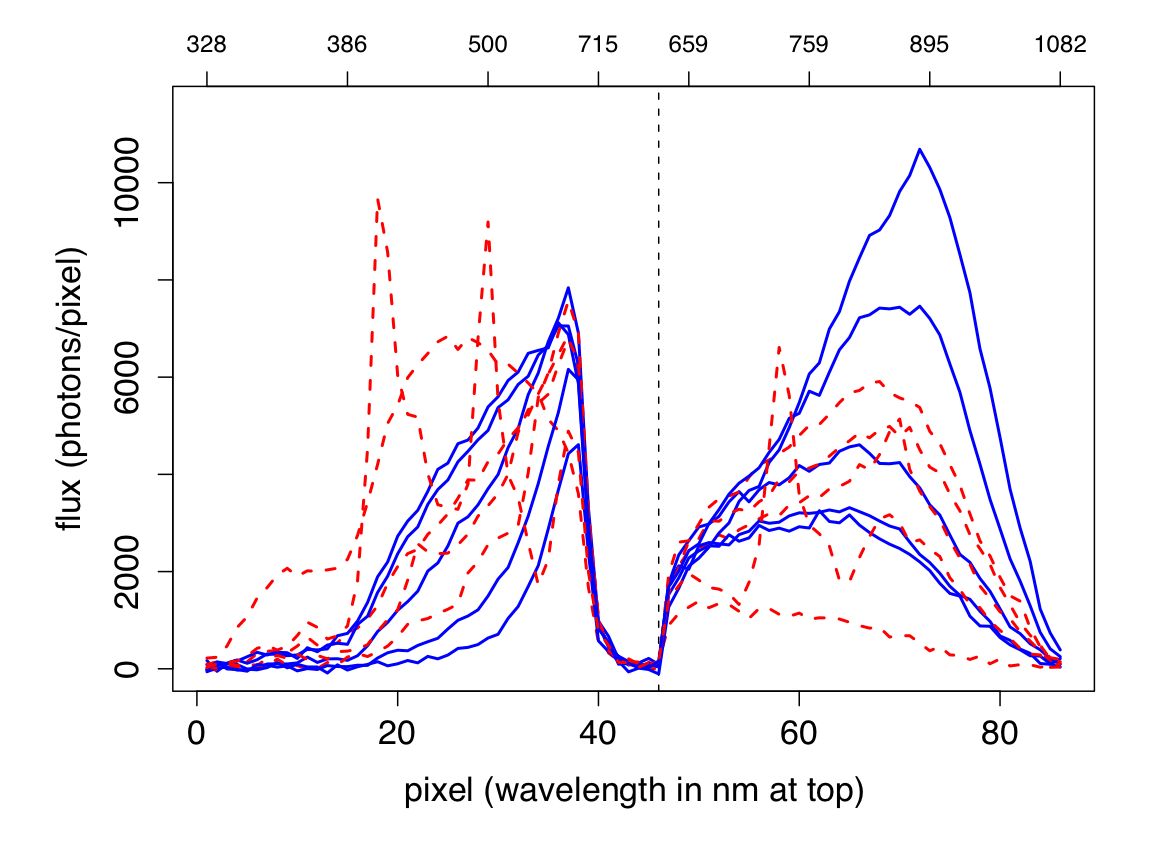
| Figure 1: Examples of the Gaia spectra for stars (blue solid lines) and quasars (red dashed lines) at G=18.5 (noise included). The spectra are plotted against pixel numbers with the wavelength scale at the top (the dispersion is nonlinear). The spectra are obtained in two channels (blue and red) using prism spectrographs. The resolution is very low, so emission and absorption lines are only visible when these features are very broad. |
The MPIA group is using existing - and developing new - pattern recognition
techniques to analyse the spectral data. Standard methods include support
vector machines, neural networks, principal component analysis and mixture
models. An estimate of the performance of our current algorithms is shown in
Figure 2.
|
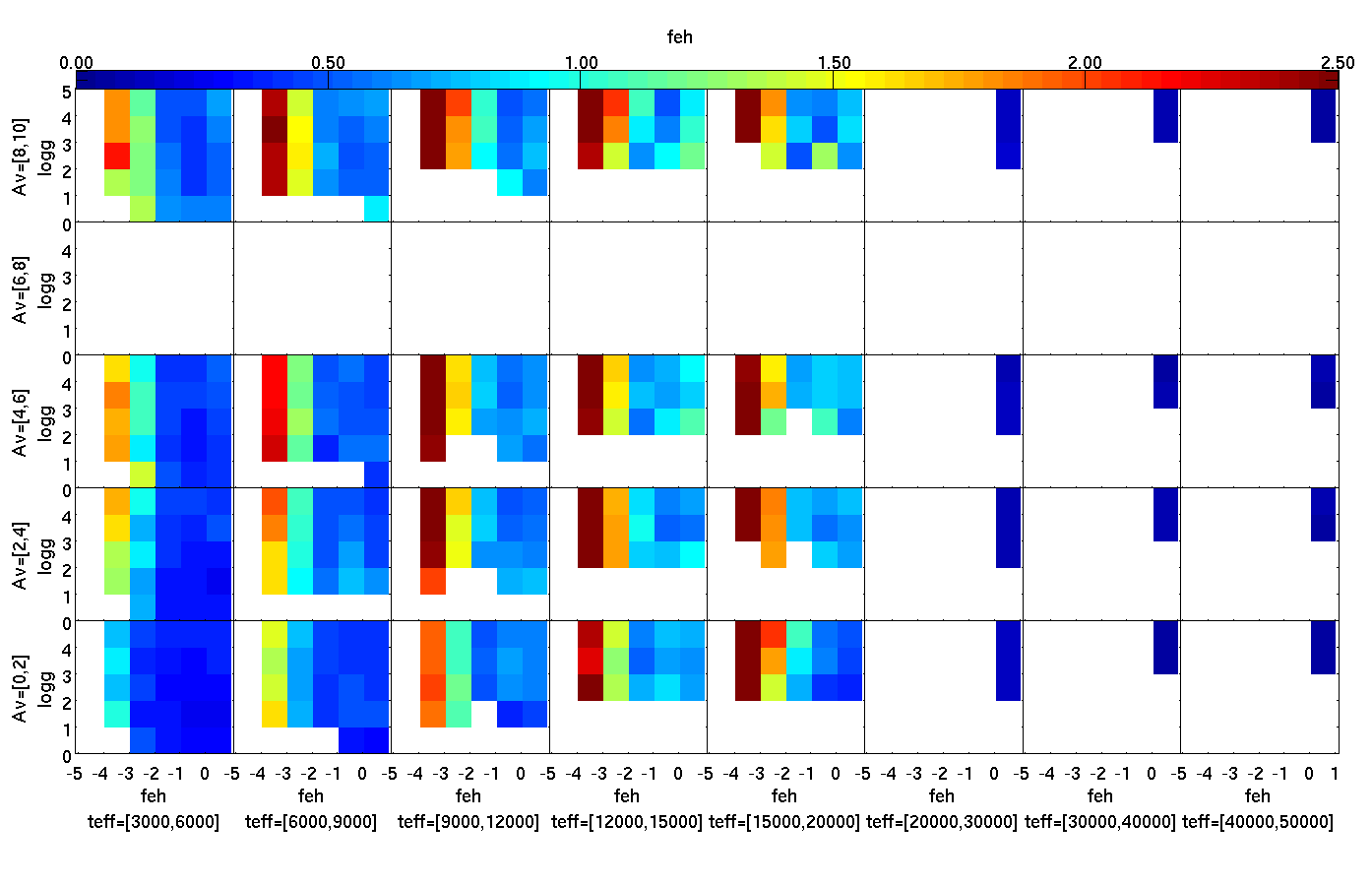
| Figure 2: Example performance of one of a Gaia stellar parametrizer (support vector machine) in determining temperature (teff), interstellar extinction (Av), metalliticy (feh) and surface gravity (logg). The outer axes plot ranges of the "strong" parameters (teff, Av), which have the most dominant effect on the spectrum. Each panel then shows, on a colour scale, the RMS error in the determination of feh as a function of the two "weak" parameters (feh, logg), for that range of Av and teff. In this way we can show the variation in accuracy over four dimensions (parameters) in a two-dimensional plot. A metallicity error less than about 0.25 dex is good, which we achieve for all cooler stars (Teff<9000K) over most of the metallicity range, and even for hotter stars with higher metallicities. (Hot stars have a much weaker metallicity signature.) What's encouraging is that this is even possible at high interstellar extinction. |
Our recent work has investigated how we can build very pure samples
of rare objects, such as quasars. (Quasars are astrophysically
interesting but will also be used to fix the Gaia astrometric
reference frame.) Classification is a probabilistic process: with
imperfect data we can rarely be 100% confident. So in building
samples of we must trade off sthe ample completeness with its
contamination. We have developed a simple but potentially powerful
method of doing this based on Bayesian principles. It adjusts the normal
classifier output probabilities to accommodate our prior expectation of the
frequency of source of different classes in a target data
set. In this way we can increase our sensitivity to rare objects (Figures
3 & 4). Our simulations suggest that we can build a sample of quasars
down to G=20 with around 50% completeness with a contamination of less
than 1 in 40 000. This translates to a sample of up to 250 000 quasars with
just 6 contaminants. Alternatively, we can build a larger (more
complete) sample if we permit a higher contamination.
|
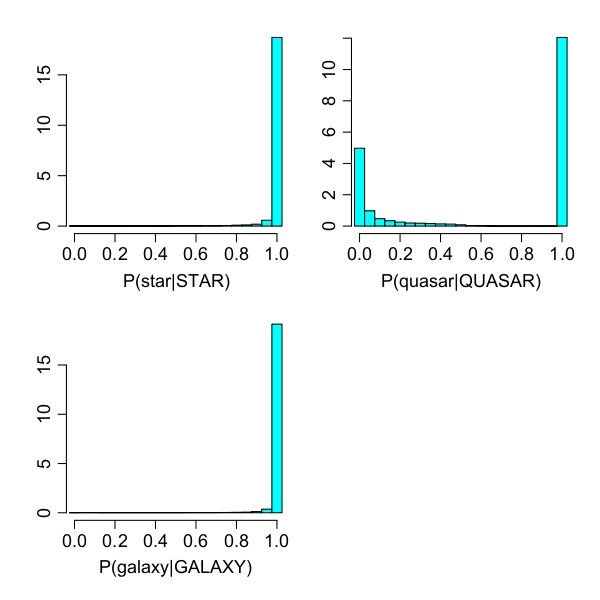
| Figure 3: Class probability estimates of the Gaia classification algorithm. Each histogram shows the probabilities assigned by the algorithm for objects truely of that class. A perfect classifier would have a peak at 1 and zero elsewhere. This shows the case in which quasars are assumed to be 1000 times rarer than stars or galaxies. |
|
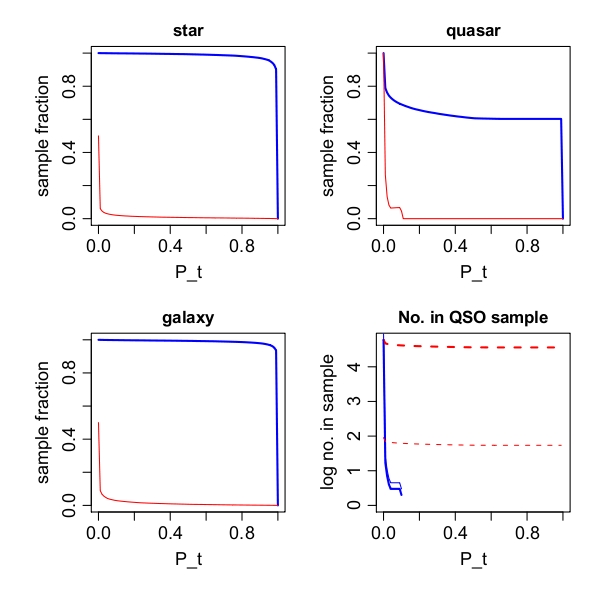
| Figure 4: Sample building with Gaia. Using an adjustable probability threshold (horizontal axis) in the classifier, we can construct samples of objects which trade off the completeness (blue line) and contamination (red line) in the sample. As the threshold increases we get more conservative in building the sample, so the contamination (fraction of false positives) decreases at the cost of a smaller completeness (fraction of true objects found). We can simultanesouly get a zero contamination quasar sample and very pure (<1% contamination) yet complete (99%) star and galaxy samples. |
A second area of investigation has been the development of a new
method for estimating parameters from spectra, called ILIUM. Most
machine learning try to solve an inverse problem, that is, determine
the parameters from the data. (It is inverse because the mapping is
not one-to-one when we have imperfect data.) In doing so, these
methods must implicitly learn the sensitivity of each data dimension
(pixel in spectrum) to the parameters. Unfortunately, due to noise
and the complexity of the problem, they don't always do this very
well. The MPIA group has developed a new method which calculates these
sensitivities explicitly using synthetic data and uses them in an
iterative scheme to estimate the astrophysical parameters (Figures 5 &
6). Preliminary results suggest that it is slightly better than
standard methods and, moreover, automatically provides information
standard methods cannot easily provide (error estimates,
goodness-of-fit, relevance of input data in determining the output).
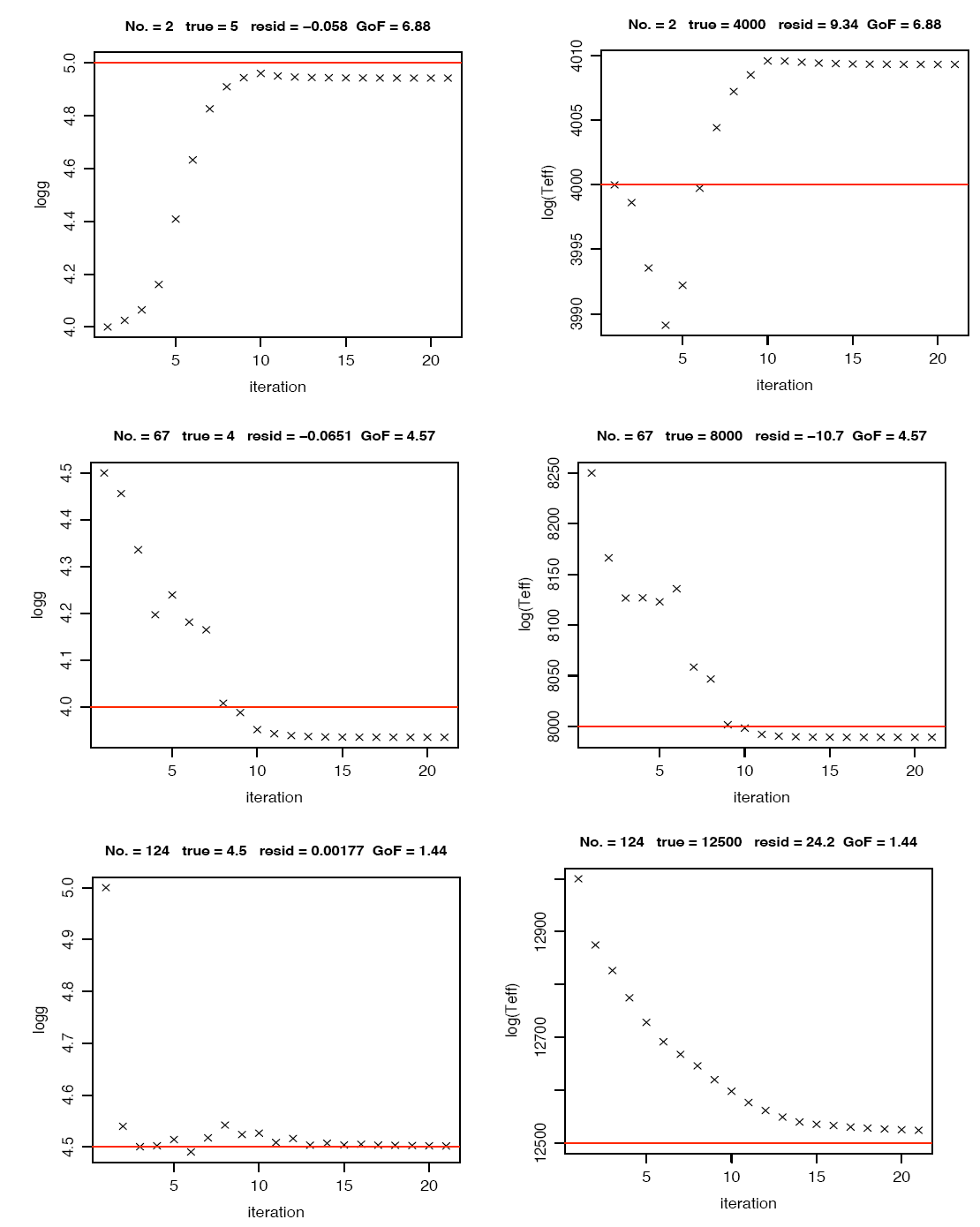
|
| Figure 5: The ILIUM algorithm estimates the astrophysical parameters of objects iteratively. The panels shows the iterative updates for three stars (the three rows) for the surface gravity parameter logg (left panels) and effective temperature (right panels). The red line shows the true parameter in each case. |
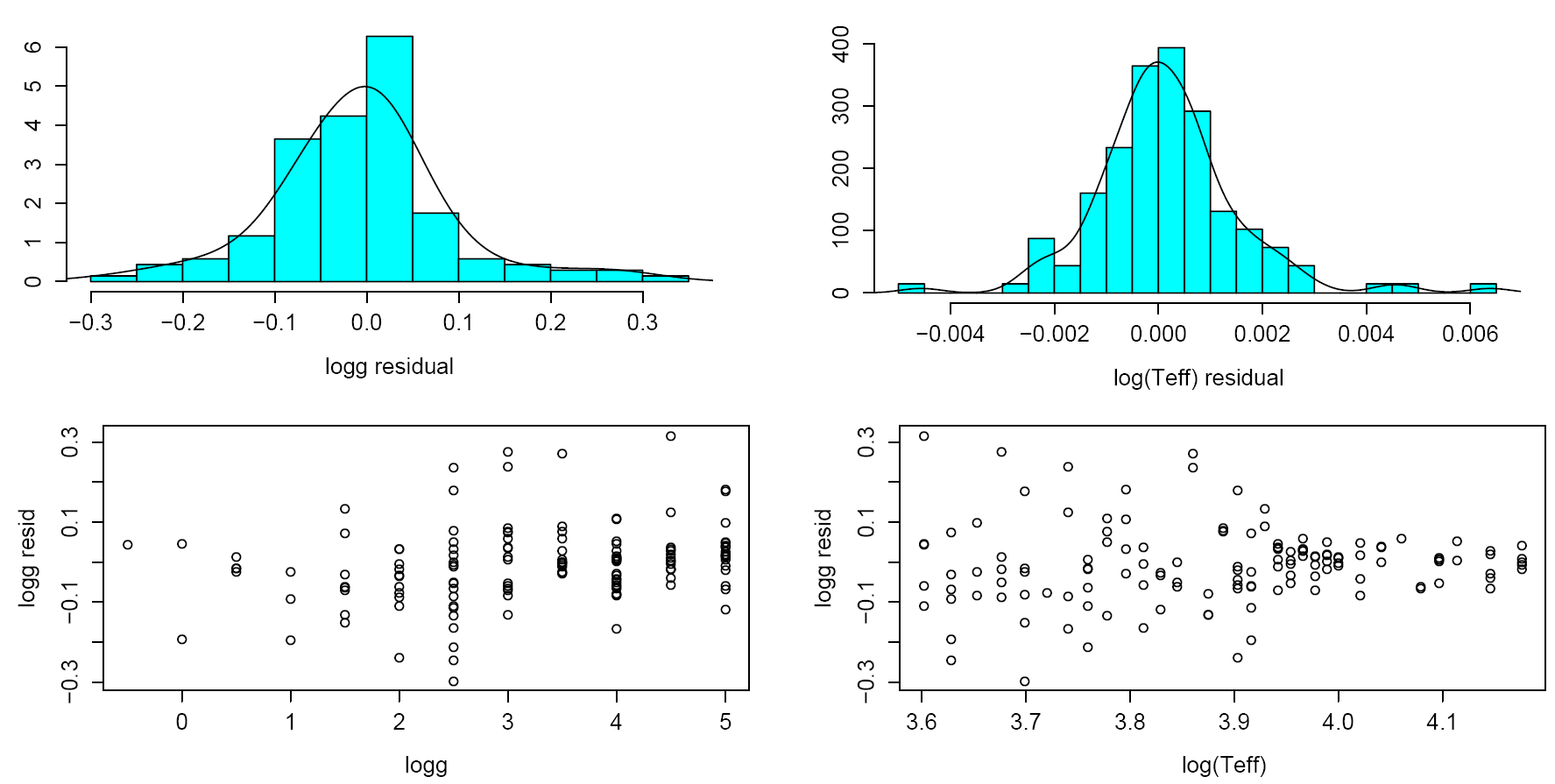
|
| Figure 6: Summary of the performance of ILIUM in estimating stellar surface gravity (logg) and effective temperature (Teff) by plotting the histogram and trends of the residuals (estimated minus true). The mean absolute errors for logg and Teff (shown here for stars at G=15) are 0.07 dex and 0.2% respectively, some five times better than a nearest neighbours algorithm applied to the same data. |
An important ingredient of all classification models is the sectral
data on which they are trained. For this we take spectra with known
astrophysical parameters and simulate the spectra using a model of the
Gaia instrument. We use a range of synthetic and real spectral
libraries for this purpose. Our group, in collaboration with
colleagues at the University of Athens and Institut d’Astrophysique de
Paris, has constructed a new library of synthetic galaxy spectra to
increase the variety of objects available for training (Figure
7). Gaia is expected to observe around one million galaxies, and using
their spectra we will be able to measure their redshifts, types and
infer some aspects of their star formation history.
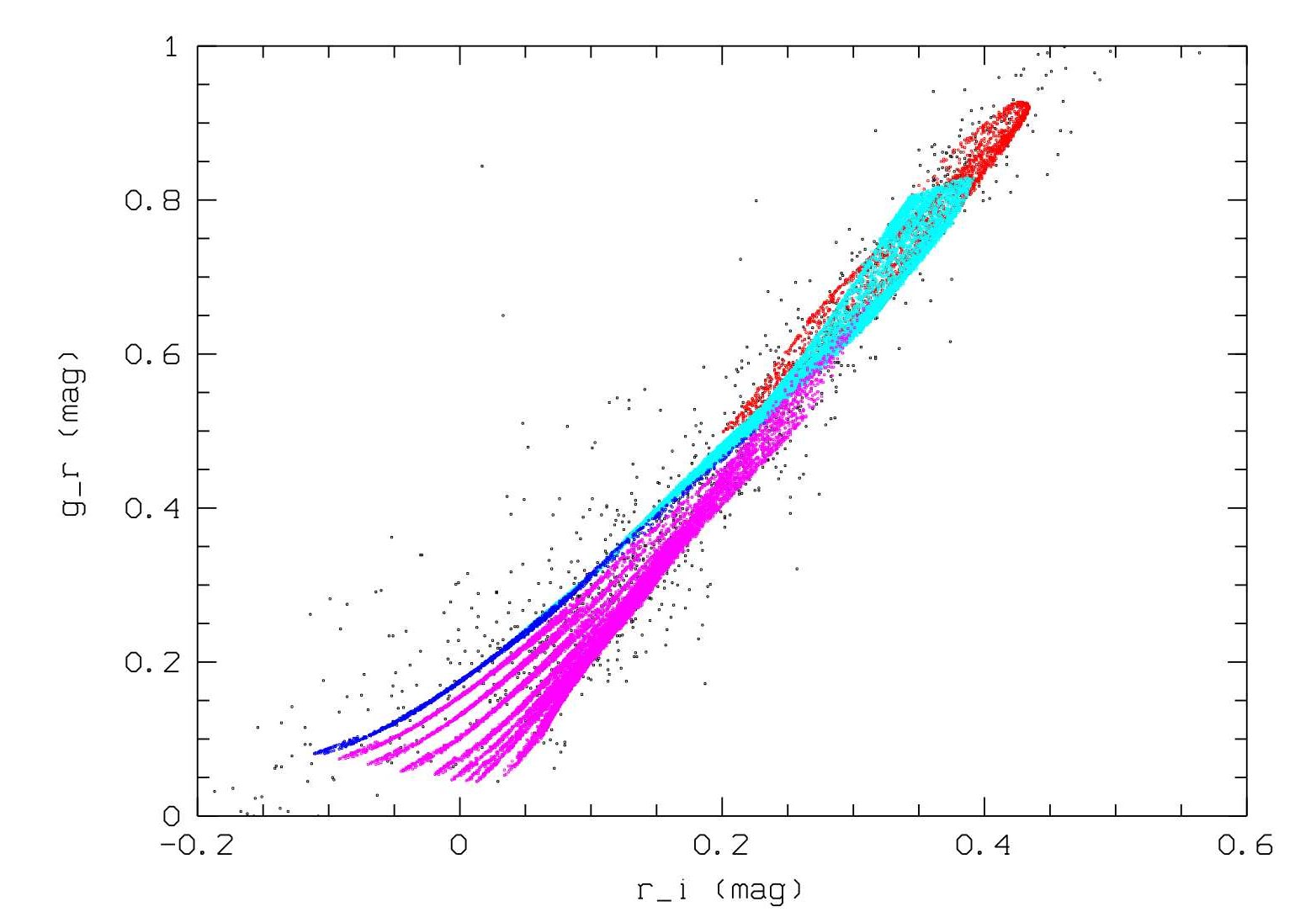
|
| Figure 7: Synthesized g-r and r-i colors for the new library of synthetic galaxy we have constructed for the Gaia classification work. Models of starburst, irregular, spiral and early type galaxies are presented with magenta, blue, light blue and red points respectively. The black points are SDSS galaxies (DR4) with z<0.01, which are used to guide the parameter settings of the models. |